CODICI BINARI
18.01.2023
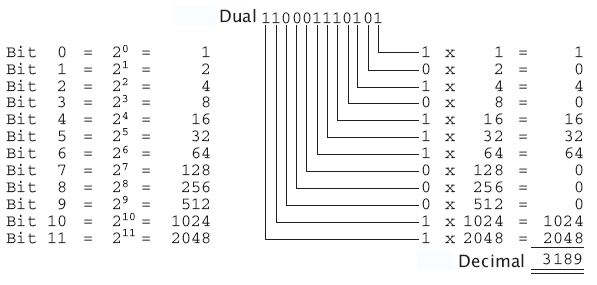
CODICE O SISTEMA BINARIO
Nel sistema binario ci si riferisce a un sistema numerico in base 2. Ossia, composto solo da due cifre (convenzionalmente 0 e 1) che nel linguaggio informatico corrispondono agli stati fisici (acceso e spento) dei transistor che compongono i vari chip. Se le cifre binarie (in inglese binary digit,"bit") diventano 8 (che nel linguaggio informatico corrispondono a 1 byte ), le combinazioni decimali (e quindi i possibili stati del sistema elettronico dei computer) salgono a 256. il codice binario sembra che non sia solamente più complesso da capire, ma anche meno efficiente: mentre quattro cifre binarie rappresentano 16 stati differenti (da 0 a 15), con 4 cifre decimali si possono rappresentare ben 10.000 stati differenti (da 0 a 9.999).

CODICE ESADECIMALE
I codici esadecimali sono numeri in base 16 e più precisamente sono: 0, 1, 2, 3, 4, 5, 6, 7, 8, 9, A, B, C, D, E, F, dove zero è pari a 0 e F è pari a 15. È spesso usato come intermediario, oppure come sistema numerico a sé stante. Per esempio, è possibile esprimere un byte con esattamente due cifre esadecimali (invece che con tre decimali).
IL CODICE ASCII
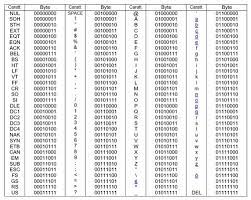
Il Codice ASCII è un codice che ci permettere di cambiare le lettere in numeri binari e viceversa. è stato codificato su 7 bit, perciò ogni carattere è formato da una stringa di 7 cifre, che combinano 0 e 1 in modo unico: a ciascun carattere corrisponde una stringa precisa. In questo modo ogni singola combinazione ha una corrispondenza univoca.
Considerando quindi che il codice binario si basa su due cifre, il codice ASCII può rappresentare non più di 2elevato a 7 simboli differenti, cioè fino a un massimo di 128 caratteri. Non tutti i caratteri ASCII sono alfanumerici: i primi 32 servono infatti per inviare comandi, perciò non sono stampabili.
Questo sistema di codifica, però, presenta alcuni limiti. Essendo stato ideato in America, infatti, non comprende tra i caratteri speciali, nessuna delle lettere accentate, in quanto non vengono utilizzate nell'ortografia della lingua inglese.Il codice ascii è ormai antiquato e quindi si usa l'un.
Il codice Ascii esteso è un'estensione del classico sistema di codifica aggiunge un bit, diventando quindi un codice a 8 bit in questo modo potremmo avere a disposizione 256 (2elevato a 8 ) caratteri: 128 sono di base, mentre i rimanenti sono caratteri speciali e grafici.
Inoltre questo sistema organizza i codici il delle "code page", delle pagine che utilizzano l'ottavo bit per aggiungere dei caratteri speciali in più al classico Codice ASCII. Questo standard di estensione prende il nome di ISO/IEC 8859-1, più semplicemente detto Latin1, per la possibilità che offre di estendersi anche ai caratteri speciali della lingua latina.
ALGEBRA DI BOOLE
L'algebra di Boole pone una soluzione ai problemi di logica.
Si basa su un enunciato che è una proposizione di cui si possa verificare se sia vera o falsa.
ENUNCIATO
Un enunciato è una cosa oggettiva ed è composto, cioè formato da due o più enunciati semplici collegati tra loro attraverso connettivi logici.
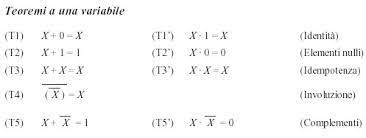
TAVOLE DI VERITÀ
Le tabelle di verità furono introdotte da Gottlob Frege, Charle Peirce, Bertrand Russell e altri verso il 1880, ed assunsero la forma attuale nel 1922, con i lavori indipendenti di Emil Leon Post e Ludwig Wittgenstein.
La tavola di verità di un connettivo è una tabella che lo caratterizza completamente descrivendo in quali casi l'espressione ottenuta"applicando"il connettivo risulta vera.
le tavole di verità verificano se un enunciato sia vero o falso e rappresentano un'espressione logica.
In una tabella di verità sono rappresentate in colonna tutte le possibili combinazioni di valori che possono assumere le variabili logiche. Le tabelle di verità applicate alla logica binaria sono limitate alla logica booleana, dove sono ammessi soltanto due valori, vero (1) e falso (0) .
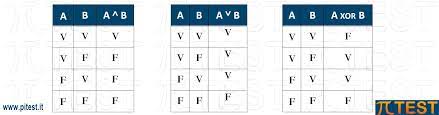
All'interno delle tavole possiamo inserire vari connettivi logici:
CONGIUNZIONE LOGICA: AND ^
DISGIUNZIONE LOGICA:OR
NEGAZIONE LOGICA:NOT
COMPLEMENTO
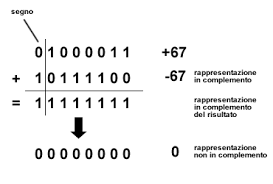
Per fare la sottrazione tra numeri binari ci si aiuta con la somma, il complemento
(qualcosa che si aggiunge)
COMPLEMENTO A 1: Complemento a uno
Il complemento a uno, o complemento alla base diminuita, è un metodo di rappresentazione dei numeri relativi in base binaria. La rappresentazione in complemento a 1 è meno usata di quella in complemento a 2 ma, per la sua facilità di calcolo, risulta molto utile nelle operazioni di sottrazione all'interno delle ALU. Si potrà indicare con 0101101: 1010010
COMPLEMENTO A 2
Il complemento a due invece basterà aggiungere 1 al risultato della somma del complemento a 1= 1010010+1